RotorFEM

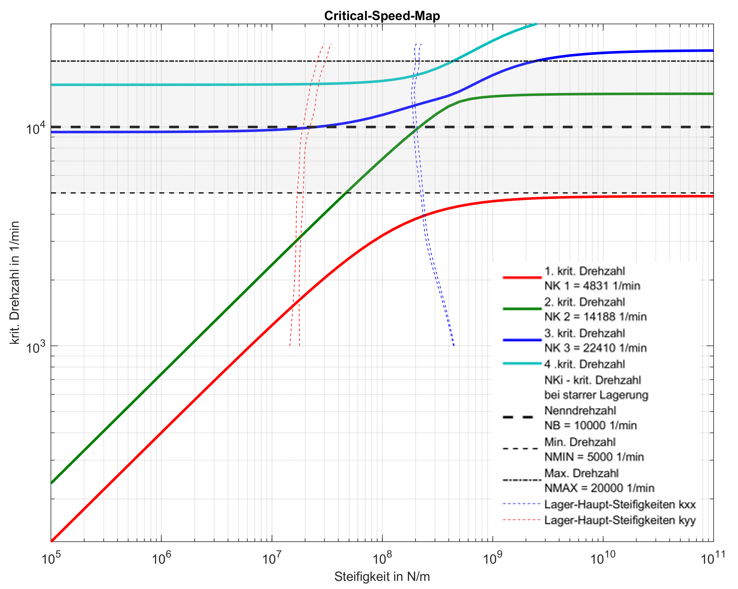
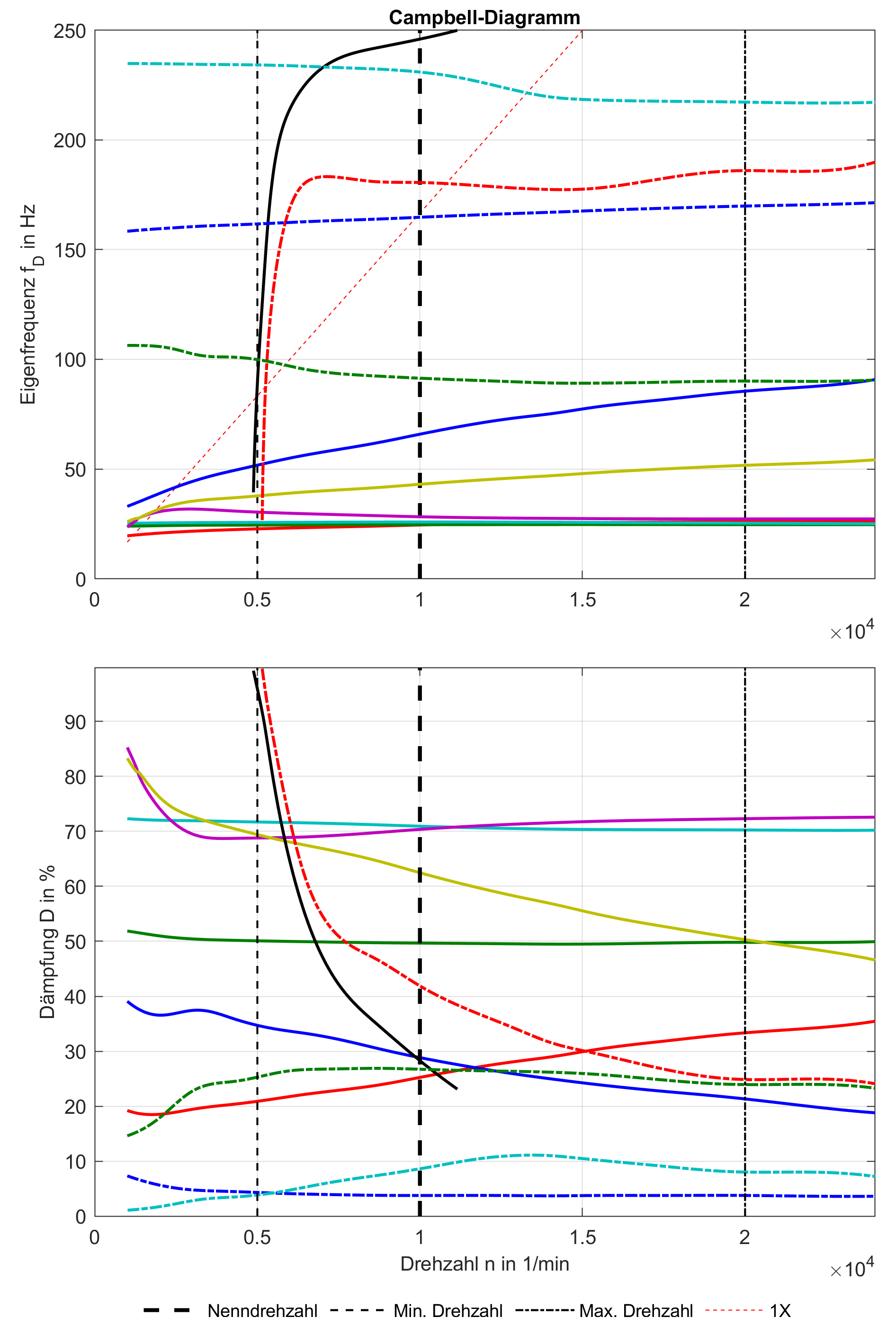
Das Berechnungsprogramm RotorFEM ermöglicht die statische und dynamische Analyse von Rotor-Lager-Systemen. Das Programm basiert auf der Methode der Finiten Elemente, wobei die Modellierung der elastischen Rotorwelle mit Timoshenko-Balkenelementen erfolgt. Das Programm ist optimal auf die Kopplung mit den Gleitlagerberechnungsprogrammen COMBROS R/A ausgelegt. Der Berechnungsumfang erstreckt sich sowohl über lineare als auch über nichtlineare Analysemethoden, wodurch das Eigen- und Zwangsschwingungsverhalten des Rotor-Lager-Systems simuliert werden kann. Dabei erfolgt eine Erstellung aller gängigen Kennwertdiagramme wie Critical-Speed-Maps, Bode-Diagramme oder Campbell-Diagramme.

Berücksichtigung der Lager- und Gehäuseeigenschaften

• Für die Berücksichtigung der Lager- und Quetschöldämpfer-Eigenschaften existieren diverse Schnittstellen (KC(M)-Modell und Kennfeld für nichtlineare Berechnungen)
• Direkte Lösung der Reynoldsgleichung für nichtlineare oder transiente Analysen
• Berücksichtigung frequenzabhängiger Lagereigenschaften durch ein Zustandsraummodell des Kippsegmentlagers
• Gehäuse/Fundament bedingte Kopplung der Lagerstellen untereinander durch Anbinden von Übertragungsfunktionen 

Statische Analysen

• Ermittlung des Gleichgewichtszustandes statisch bestimmter und statisch überbestimmter Systeme als Ausgangspunkt für die dynamischen Analysen
• Berechnung der Wellenverlagerung und der Lagerkräfte

Eigenwertanalysen

• Berechnung der Eigenwerte und Eigenvektoren des linearisierten Systems
• Auswertung von Frequenz und Dämpfungsgrad
• Bestimmung der Stabilitätsgrenze
• Auswertung der Schwingform bezüglich Richtung und Umlaufsinn (Gleich- und Gegenlauf)
• Sortierung der Eigenwerte durch einen heuristischen Algorithmus
• Generierung aller gängigen Kennwertdiagramme (Campbell-Diagramm, Critical-Speed-Map…)

Harmonische Analysen

• Drehzahlsynchrone Unwuchterregung inklusive Momentenunwucht
• Beliebige harmonische Anregung (Amplitude, Richtung, Phase)
• Auswertung von Amplitude und Phase der Bewegung und der Reaktionskräfte
• Auswertung der Bahnkurven und der Schwingform
• Generierung aller gängigen Kennwertdiagramme (Frequenzgang-Diagramme für Weg- und Kraft-Amplituden, relative Lagerschwingungen)
• Verifizierung der Linearitätsannahme durch Lagerkoeffizienten dritter Ordnung (ermittelt durch Störungsgleichungen dritter Ordnung der Reynoldsgleichung)
• Auswertung des Amplitudengangs nach dem API Standard

Nichtlineare Analysen

• Berechnung des Schwingungsverhaltens unter Berücksichtigung der nichtlinearen Lagerkräfte
• Kennfeldverfahren oder direkte Lösung der Reynoldsgleichung
• Iteratives Verfahren zur Berechnung eines quasistatischen Zustandes (harmonischer Ansatz)
• Zeitintegrationsverfahren (ansatzfreie Lösung)
• Pfadverfolgung bei Koexistenz mehrerer Lösungen