RotorFEM

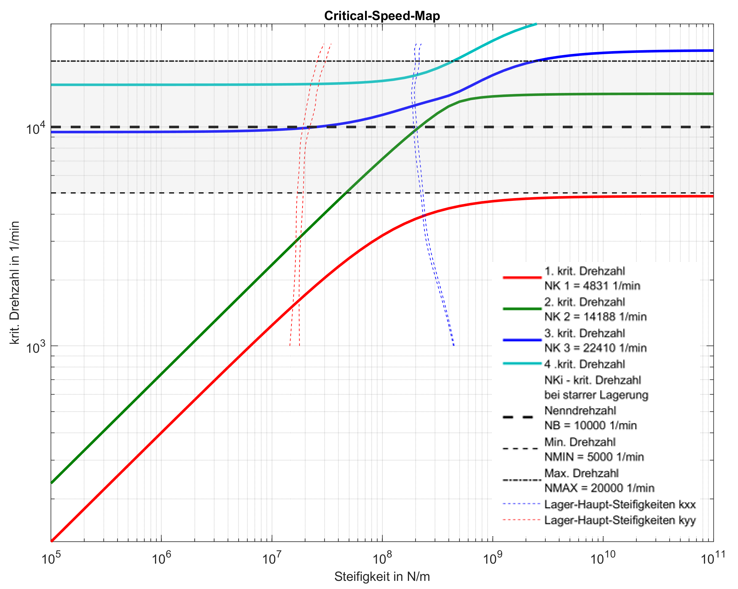
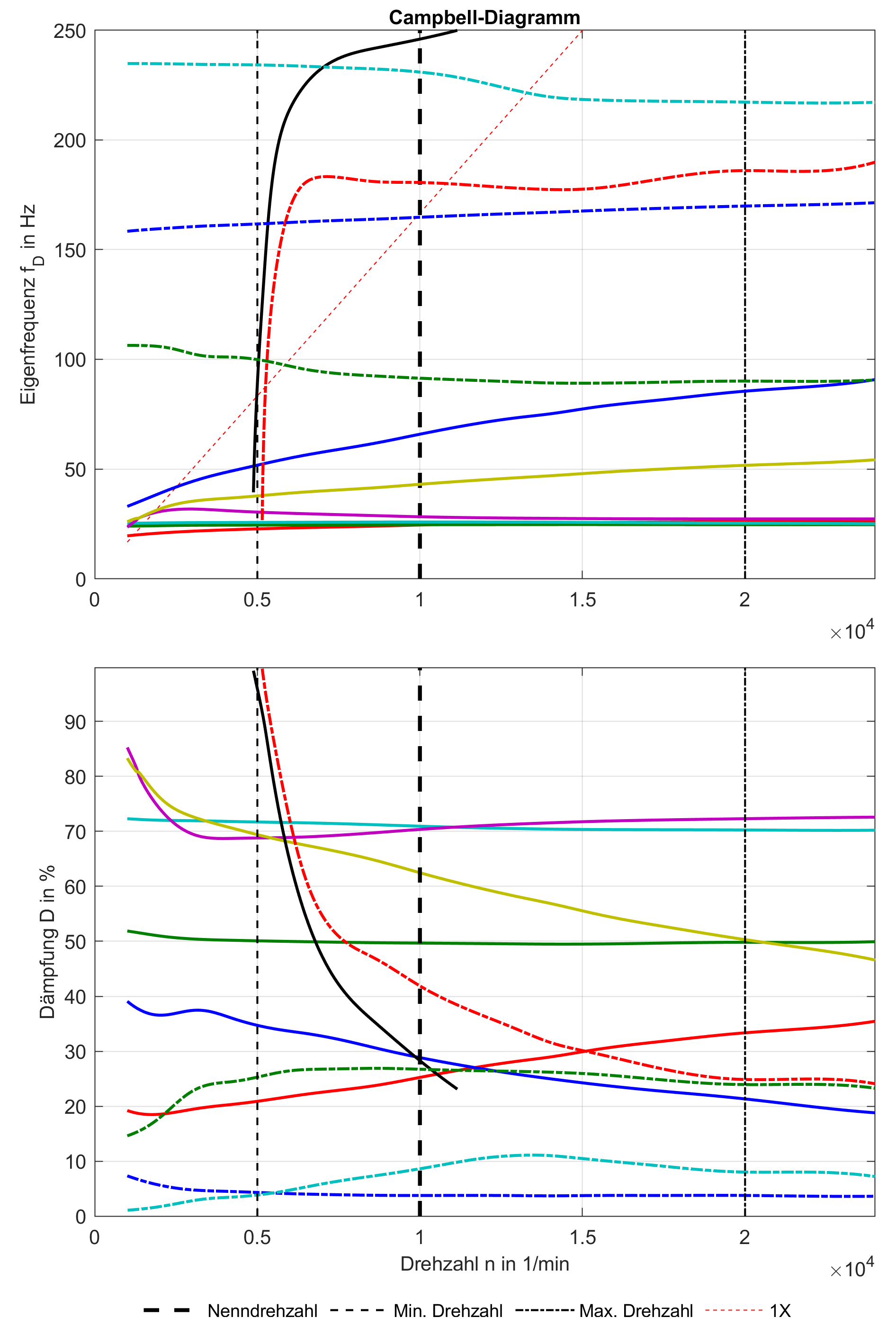
The RotorFEM calculation program enables the static and dynamic analysis of rotor-bearing systems. The program is based on the finite element method, whereby the elastic rotor shaft is modeled using Timoshenko beam elements. The program is optimally designed for coupling with the COMBROS R/A plain bearing calculation programs. The scope of calculation covers both linear and non-linear analysis methods, allowing the natural and forced vibration behavior of the rotor-bearing system to be simulated. All common characteristic value diagrams such as critical speed maps, Bode diagrams or Campbell diagrams are created.

Consideration of bearing and housing properties

• Various interfaces (KC(M) model and map for non-linear calculations) are available for taking the bearing and squeeze oil damper properties into account
• Direct solution of the Reynolds equation for non-linear or transient analyses
• Consideration of frequency-dependent bearing properties using a state space model of the tilting pad bearing
• Housing/foundation-related coupling of the bearing points with each other by linking transfer functions

Static analyses

• Determination of the equilibrium state of statically determinate and statically overdetermined systems as a starting point for the dynamic analyses
• Calculation of shaft displacement and bearing forces

Eigenvalue analyses

• Calculation of the eigenvalues and eigenvectors of the linearized system
• Evaluation of frequency and degree of damping
• Determination of the stability limit
• Evaluation of the mode of vibration with regard to direction and direction of rotation (synchronous and counter-rotation)
• Sorting of the eigenvalues using a heuristic algorithm
• Generation of all common characteristic value diagrams (Campbell diagram, critical speed map...)

Harmonic analyses

• Speed-synchronous unbalance excitation including torque unbalance
• Any harmonic excitation (amplitude, direction, phase)
• Evaluation of amplitude and phase of the movement and the reaction forces
• Evaluation of trajectory curves and vibration mode
• Generation of all common characteristic value diagrams (frequency response diagrams for displacement and force amplitudes, relative bearing vibrations)
• Verification of the linearity assumption using third-order bearing coefficients (determined using third-order perturbation equations of the Reynolds equation)
• Evaluation of the amplitude response according to the API standard

Non-linear analyses

• Calculation of the vibration behavior taking into account the non-linear bearing forces
• Map method or direct solution of the Reynolds equation
• Iterative method for calculating a quasi-static state (harmonic approach)
• Time integration method (approach-free solution)
• Path tracking with coexistence of several solutions